Až si postavíte prvního robota pro SUMO a pustíte jej samotného na hřiště bude se pravděpodobně pohybovat tak, že pojede rovně, narazí na okraj, otočí se a pojede zase rovně dokud znovu nenarazí na okraj. Takhle se pohybuje většina robotů pro SUMO. Abyste měli šanci zvítězit, je velice důležité, aby se váš robot držel co nejvíce ve středu hřiště.
Je daleko lepší, když robot jezdí, jak je nakresleno žlutou čarou, než když se pohybuje u okraje a může být vytlačen, jak je nakresleno modrou čarou.
Přestože většina SUMO robotů vůbec neví, kde na hřiští je, existuje metoda jak robota nasměřovat na střed hřiště, tak aby z kterékoliv polohy, nejpozdeji při druhé otáčce zamířil přesně na střed hřiště.
Pokud uvažujeme jak to udělat, je třeba si uvědomit, že při jízdě robota známe jenom dvě věci – průměr hřiště, který je 77,5 cm a ujetou dráhu od minulé otočky. Tuto délku můžeme stopovat jako čas od poslední otočky a uložit si ji v programu robota do nějaké proměnné. Podílem těchto dvou čísel získáme úhel alfa, který svírá naše dosavadní dráha se směrem ke středu hřiště. Úhel alfa vypočteme podle vzorečku:
Cos (alfa) = Ujetá vzdálenost / Průměr hřiště
Úhel o který je třeba otočit vypočteme jako:
beta = 180 – alfa
Takže robot, když narazí na okraj hřiště, se neotáčí náhodně, ale vypočte si úhel a o ten otočí. Přesto použití kosinu je pro malé procesory v SUMO robotech trochu složité, proto jsem vypočetl tuto tabulku:
|
Ujetá vzdálenost |
Úhel otočení |
Dráha otočení |
|
0 |
90,0 |
7,9 |
|
10 |
97,4 |
8,5 |
|
20 |
105,0 |
9,2 |
|
30 |
112,8 |
9,8 |
|
40 |
121,1 |
10,6 |
|
50 |
130,2 |
11,4 |
|
60 |
140,7 |
12,3 |
|
70 |
154,6 |
13,5 |
|
77,5 |
180,0 |
15,7 |
Poslední sloupec dráha otočení vychází z toho, že robot má o něco méně než 10 cm (viz pravidla Mini Sumo) a v tabulce je dráha, kterou musí ujet jedním kolečkem dopředu a druhým kolečkem dozadu, aby otočil o potřebný úhel.
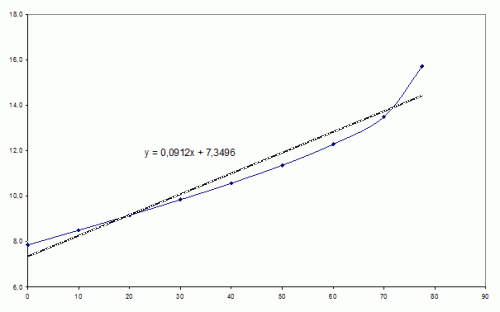
Většina robotů pro SUMO ale nemá měření ujeté vzdálenosti, také my nebudeme měřit vzdálenost, ale máme v programu jenom proměnnou s ujetým časem. I s tím se dá něco dělat. Pokud si ujetou vzdálenost a dráhu otočení vykreslíme do grafu, získáme tuto křivku
Jak vidíte, křivkou jde docela dobře proložit přímka a její rovnici máme v grafu. Z rovnice i z tabulky vyplývají dvě věci, které nám výpočet velice usnadní:
1. Je třeba otočit minimálně o ¼ kruhu (90 stupňů)
2. Kromě toho je třeba za každý ujetý centimetr po hřišti točit kolečky ještě 0,091 cm
Abychom si usnadnili výpočet, přijmeme ještě nějaká další zjednodušení a konečný vzoreček bude:
DOBA OTÁČENÍ = DOBA ¼ OTÁČKY + (DOBA OD MINULÉ OTOČKY) / 8
Proč místo násobení 0,0912 dělíme 8 ? – Protože dělení 8 je pro procesory velmi snadné a jde to (bitovým posunem) udělat i v assembleru.
Dobu otočení Vašeho robota musíte změřit – nejlépe tak že jej necháte točit na místě 10x a čas vydělíte 10. Pří otáčení mají kolečka robotů tendenci prokluzovat, proto zkuste co se stane, když místo dělení 8 dáte dělení 4 – u některých robotů to bude fungovat ještě lépe.
Pokud má váš robot čidla soupeře – nenechávejte jej točit na místě, dokud soupeře „neuvidí“, protože to vede k tomu, že oba roboti se točí na své polovině hřiště a „čekají“. Lepši je jezdit rovně přes střed a pokud přitom uvidím soupeře otočit a jet mu „naproti“.
Pokud naměřený čas je výrazně delší než čas potřebný pro přejetí hřiště – je jasné, že robot se cestou „přetlačoval se soupeřem“ v takovém případě je lepší otočit naslepo o necelou polovinu kruhu a otočku počítat až při příštím střetu s okrajem hřiště.
S tímto způsobem navigace se vaši roboti nebudou potácet na okraji arény a bude pro ně mnohem snazší zvítězit a to i tehdy pokud nebudou mít čidla soupeře, nebo pokud jej při jízdě neuvidí.