V poslední zdvojené části tohoto seriálu nás čeká několik pokusů, které s naší postavenou technikou a běžně dostupnými „zářiči“ můžeme dělat. Budeme si zkrátka hrát se zářením.
Co dál?
Celý dosavadní postup měl za cíl naučit se detekovat a měřit ionizační záření vlastnoručně postaveným zařízením jednou co nejjednodušeji a nejlevněji, podruhé třeba s co největší citlivostí. Toho jsme dosáhli, můžeme se soustředit na pokusy, které by představily některé z vlastností záření. Jdeme si tedy hrát, ač spojení „hrát si s radiací“ je určitě hodně nezvyklé a provokativní. Není to konec konců nic jiného, než jednoduché školní pokusy, které však nyní můžeme realizovat sami.
Vliv vzdálenosti
Jestliže budeme mít rozměrově malý (teoreticky bodový) zdroj záření a nebude docházet k pohlcování prostředím, pak by intenzita záření měla být nepřímo úměrná druhé mocnině vzdálenosti. Pokusíme se to ověřit. V praxi to znamená, že když budeme od zdroje záření 2x dál, bude intenzita 4x nižší, budeme-li 4x dál, intenzita klesne 16x atd.
Výchozí podmínky se nám nepodaří splnit, ale musíme se snažit se jim přiblížit. Jako zářič použijeme punčošku do lampy nebo lépe dvě na sobě kvůli zvýšení aktivity, připevníme je na boční stěnu nějaké krabičky, aby byly kolmo na GM trubici a posunováním krabičky se dala snadno měnit vzdálenost. Punčoška generuje záření α, β i γ, ale α neprojde do GM trubice a γ záření je relativně málo, převládající je β. Vzdálenosti a hodnoty se mohou lišit podle konkrétních podmínek, zde je popis uskutečněného kontrolního pokusu.
Improvizované měření vlivu vdálenosti
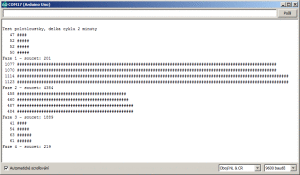
Použijeme stejný detektor s GM trubicí spojený s Arduinem jako při předchozí práci, program mírně upravíme. Budeme snímat celkem 4 série po 4 měřicích cyklech, každý cykl bude trvat 2 minuty. Vzhledem ke krátké době měření lze očekávat, že výsledky budou jen přibližné. První série bude kontrola pozadí, druhá zářič na vzdálenost 20 cm, třetí na 10 cm a poslední série opět kontrola pozadí bez zářiče. Výsledek vykreslený znaky sériového monitoru je na obrázku. A jak to vyšlo číselně?
Vliv vzdálenosti od „zářiče“
Kontrola pozadí na začátku zaznamenala celkem za 8 minut 241 pulzů, na konci za stejnou dobu 211 pulzů, průměr je 226 pulzů, ten odečteme jako korekci měření se zářičem. Při vzdálenosti 20 cm se zaznamenalo celkem 1316 pulzů, po korekci to je 1090 pulzů. Všechny cykly jsou velmi dobře vyrovnané. Při 10 cm odstupu bylo zaregistrováno 4792 pulzů (po korekci 4566 pulzů). Podle očekávání by měl být poměr počtu pulzů po korekci 1:4 tedy 0,250, měřením vyšlo 0,239, to je myslím s ohledem na podmínky domácího pokusu a statistický charakter intenzity záření velmi slušná shoda.
Určení polotloušťky materiálu
Jestliže záření prochází nějakým prostředím, které jej pohlcuje, a nedochází ke vzniku sekundárních emisí, pak nás zajímá, jaká tloušťka materiálu zeslabí intenzitu záření na polovinu. Tato tloušťka daného materiálu se nazývá polotloušťka. Když dáme do cesty záření překážku 2x silnější, zeslabí se záření na ½ x ½ = ¼.
Obvykle se setkáme s údaji o polotloušťce materiálů vzhledem k záření γ, my ale máme „zářiče“ s převahou β záření, kromě toho, olověné nebo železné desky silné několik centimetrů pro stínění γ záření by se nám špatně sháněly a s překážkami silnými desítky centimetrů (např. z dostupné vody) se nepohodlně pracuje. β záření má mnohem menší pronikavost a tak můžeme využít toho, co každý z čtenářů tohoto článku má, totiž výtisku časopisu Praktická elektronika*. Od čísla 12/2015 je časopis tištěn na papíře, který má 60 g/m2 a normovanou tloušťku 0,06 až 0,07 mm (změřeno 0,067 mm). To je o něco méně než standardní kancelářský papír do tiskáren a kopírek (80 g/m2). Obálce časopisu se vyhneme, časopis nemusíme nijak upravovat a nepoškodí se.
- Poznámka: Článek byl původně psán pro časopis Praktická elektronika, takže uvedená čísla platí pro něj. Pro jiný časopis nebo knihu můžeme použít stejnou metodu, ale výsledek vyjde číselně jinak.
Uspořádání pracoviště bude naprosto stejné jako při předchozím měření, nastavíme vzdálenost punčošky (nebo jiného zářiče) od GM trubice přibližně 10 cm a tato vzdálenost se nebude měnit. Obálku časopisu rozevřeme a otočíme, vnitřní listy sepneme kancelářskou svorkou a vsuneme mezi zářič a trubici. V této poloze musíme časopis nějak upevnit, postačí u hřbetu postavit z obou stran nějaké těžší předměty, třeba konzervy.
Program opět snímá 4 fáze po 4 cyklech, každý má 2 minuty. Změříme pozadí, potom intenzitu od zářiče bez vložené překážky, intenzitu s vloženou překážkou tvořenou vnitřními listy časopisu. Nakonec opět změříme pozadí. Výsledky pokusu jsou na obrázku. Počet registrovaných částic bez překážky byl v průběhu osmiminutové fáze 4384, po odečtení pozadí (210) 4174 pulzů. Přes papír prošlo 1679 částic (po korekci), takže 28 listů papíru zeslabilo záření s faktorem 0,4023. Vnitřní listy jednoho časopisu jsou tedy víc než jedna polotloušťka daného typu papíru.
Měření polotloušťky papíru
Kolik listů časopisu Praktická elektronika odpovídá polotloušťce? Podíl jednoho listu na pohlcení záření odpovídá koeficientu 28. odmocnina z čísla 0,4023. Pro počet listů (N) polotloušťky musí platit rovnice 0,4023 ^ (1/28) = 0,5 ^ (1/N), z toho N = 28 x log(0,5) / log(0,4023). N vychází 21,3 a protože počet listů těžko může být desetinné číslo, 21 listů by mělo být méně než polotloušťka, 22 listů více. Pokud by šlo o polotloušťku v milimetrech, tak 21,3 x 0,067 = 1,4 mm (přibližně). Kdo si to chce ověřit, může snížit počet vsunutých listů na 21 a měřit déle, aby byl výsledek přesnější, pak případně ještě počet zkorigovat.
Podobným způsobem můžeme změřit polotloušťku prakticky jakéhokoli materiálu. Možná překvapí, jak účinně je záření β pohlcováno parafinem (svíčkami) ale dokonce i pěnovými plasty, nemusí jít hned o kovy. Například samotná 10 cm silná vrstva lehkého pěnového polystyrenu v zateplení budovy zeslabí záření 2x. Stále se však jedná o záření β, ne o pronikavé γ záření, to by bylo vše jinak! Při jaderném výbuchu opravdu nemá smysl schovávat se za svíčku.
Věci kolem nás
K přidržení časopisu v průběhu minulého měření jsme použili konzervy, nemůže to na ně mít vliv? Půjdou potom ještě jíst? Konzervy stály bokem a intenzita záření, která na ně dopadala z punčošky, byla asi třetinová proti překážce (změřeno). Vložením zářiče do prázdné konzervy stejného typu se ukázalo, že konzervový plech propustí jen asi ¼ záření (β), dohromady to dělá útlum asi 12x. Když postavíte stejnou konzervu na žulové schody do sklepa a necháte ji tam jeden den, může dostat větší dávku, než při popisovaném měření. Dá se to snadno ověřit.
Otázka, jestli měření s naším zářičem (punčoškou) konzervu nezničí, napadne asi každého. Je to přirozené, pochopitelné a rozumné. Ale uvažujete takto, i když stavíte konzervu na schody, když sedíte ve sklípku s žulovým obkladem? Nebo když jíte ovoce, které bylo několik tisíc kilometrů přepravováno letecky ve velké výšce? Nyní máte prostředky k tomu na podobné otázky hledat a najít odpovědi. Na jednu z nich se ještě podíváme.
Byly doby, kdy se říkalo, že televizní přijímač, zejména barevný (ještě ten s vakuovou obrazovkou, ne moderní LCD, LED nebo OLED), vydává nebezpečné záření. Později se totéž říkalo o počítačových monitorech. Ono to má svou logiku, elektronový paprsek, jímž se kreslí na luminofor obrazovky, je vlastně β záření.
Zkusil jsem, zda jde něco naměřit v bezprostřední blízkosti přední strany obrazovky (TV Thomson). Výsledek dost překvapil. Opravdu to jde, před sklem obrazovky GM trubice registrovala ve vypnutém stavu (po dlouhém odstavení) dvojnásobný počet částic, než odpovídalo pozadí v okolí. Po zapnutí a delším chodu se ale překvapivě hodnoty nezměnily ani tak, jak to dokázal obyčejný banán. Vypadá to, že průnik elektronového paprsku ven z obrazovky je výborně odstíněný, ale na luminofor se používají materiály, které mají sice malou, nicméně prokazatelnou aktivitu.
Ověření statistického charakteru
Způsobuje-li přirozené pozadí na daném místě řekněme průměrně 20 impulzů v GM trubici za minutu, pak si můžeme položit otázku, jak je pravděpodobné, že naměříme za minutu přesně 20 impulzů, nebo jak je pravděpodobné, že naměříme pulzů 15. Nezáleží na tom, jestli budeme skutečně měřit pozadí, nebo jestli použijeme některý z našich zářičů, třeba korálky z uranového skla. Rozdíl je jen v tom, že při silnějším záření může být interval sledování (to budeme muset mnohokrát opakovat) kratší a práce se zrychlí.
Použijeme stále stejný detektor s GM trubicí připojený k Arduinu i uspořádání pracoviště (punčoška jako zářič ve vzdálenosti asi 10 cm), jen výsledky budeme vyhodnocovat jinak. Budeme mnohokrát měřit v kratším, třeba jen několikasekundovém intervalu. Je celkem jedno jak dlouhém, ale stále stejném. Má-li výsledek vyjít názorně, měly by být intenzita záření a interval zvoleny tak, aby průměrný počet pulzů byl asi tak 50. Vždy dostaneme nějaký počet pulzů. Budeme zjišťovat a pamatovat si, kolikrát jsme v intervalu dostali přesně 1 pulz, 2 pulzy … až 100 pulzů. Výsledky pak zobrazíme a bude nám k tomu stále stačit znaková grafika sériového monitoru.
V programu je vytvořené pole pro 71 možností počtu zachycených pulzů, jeden cyklus měření trvá 3 sekundy, graf se překreslí pro 100 cyklech. Parametry byly nastaveny podle toho, že průměrný počet částic předem změřený během krátké doby jen několika cyklů se pohyboval kolem 35 za 3 sekundy.
// Zkouska statistickeho rozlozeni - GM trubice
unsigned int pocet = 0; // promenna pro nacitani pulzu
unsigned int per = 0; // citac mereni
unsigned long time; // sledovani casu
unsigned long delka_cyklu = 3; // delka cyklu v sekundach
unsigned int stat[71]; // pole pro rozlozeni
unsigned int zobrazeni = 100; // po kolika merenich se zobrazuje
void setup() {
pinMode(2, INPUT); // pin 2 vstup GM
pinMode(7, OUTPUT); // pin 7 zvuk na piezo
pinMode(13, OUTPUT); // pin 13 LED
for (int i = 0; i <= 70; i++) { // vynulovani pole
stat[i] = 0;
}
Serial.begin(115200); // nastaveni seriove komunikace
Serial.println(" "); // odradkovani pri resetu
}
void nacti() { // obsluha int0 prisel pulz
pocet = pocet + 1;
}
void loop() {
per++;
pocet = 0; // novy cyklus
time = millis() + (delka_cyklu * 1000); // cas konce
attachInterrupt(0, nacti, RISING); // nastaveni interruptu
while (time > millis()) {
delay(1);
} // cekani na konec cyklu
detachInterrupt(0); // odpojit interrupt
stat[pocet]++; // mereni zaclenim do pole
if (per % zobrazeni == 0) {
vykresleni();
pip();
}
}
void pip() {
tone(7, 1600, 10);
noTone;
}
void vykresleni() {
Serial.print(" Test statistickeho rozlozeni po ");
Serial.print(per);
Serial.println(" merenich");
unsigned int maximum = 0;
for (int i = 0; i <= 70; i++) { // hledani maxima v poli
maximum = max(maximum, stat[i]);
}
maximum = maximum / 10;
unsigned int hodnota = maximum;
for (int j = maximum; j > 0; j-- ) {
Serial.print(" +"); // levy okraj grafu
for (int i = 0; i <= 70; i++) { // vykresleni radky grafu
if ((stat[i] / 10) >= hodnota) {
Serial.print("#");
} else {
Serial.print(" ");
}
}
hodnota--;
Serial.println(" "); // konec jednoho radku
} // konec grafu
Serial.print(" +"); // posledni radek
for (int i = 0; i < 7; i++) {
Serial.print("---------+");
}
Serial.println(" "); // konec posledniho radku
Serial.println(" "); // 3 volne radky
Serial.println(" ");
Serial.println(" ");
}
Graf na dalším obrázku získaný po 6400 měřicích cyklech (více než 5 hodinách měření) ukazuje výsledné rozložení. Teoreticky jsou možné jakékoli odchylky včetně nuly, v praxi můžeme počítat s tím, že vzhledem k průměrnému počtu registrovaných částic je pokles i nárůst o více než 1/3 dost vzácný.
Statistické rozložení
Energetické spektrum částic
Vrátíme se k detekci β částic fotodiodou BPW34 a budeme vycházet ze zapojení, které tu už bylo uvedeno.
Už jsme poznali, že pulzy na výstupu mají téměř konstantní délku zhruba 0,1 ms a jejich amplituda je úměrná energii částice, v našem případě elektronu, respektive velikosti laviny, kterou elektron svou energií v materiálu fotodiody spustil. Bohužel jednotlivá γ kvanta vytvoří příliš slabý signál, ten nejspíš zůstane v šumu, naopak α částice, které by vybudily podstatně větší impulzy než elektrony, se na neupravenou fotodiodu nedostanou přes její plastové pouzdro. Nebudeme se snažit konkurovat analyzátorům za stovky tisíc dolarů a měřit přesně energii částic v keV nebo MeV, pro začátek nám postačí sledovat zastoupení různě energeticky bohatých elektronů.
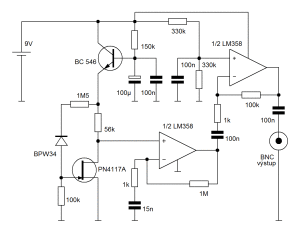
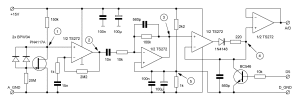Zapojení upravíme tak, abychom získali pulzy s amplitudou až 2 V, nové je na předchozím obrázku. Zvýšíme napájecí napětí na 15 V, tím se zvýší i citlivost. Použijeme dvě fotodiody paralelně, větší počet zachycených částic se při použití slabých zářičů hodí. V bodě (1) by mělo být napětí 6 až 8 V proti zemi A_GND, případně jej dostavíme změnou odporu v D. V zapojení jsou použity 4 OZ, dvě pouzdra TS272. První stupeň zesílí krátké pulzy až 2000x, nízké frekvence (zejména síťový brum) mnohem méně. Jak vypadají pulzy v bodě (2) ukazuje další obrázek.
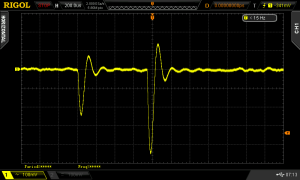O další omezení nízkých kmitočtů se postará vazební kondenzátor s malou kapacitou (10 n). Druhý stupeň zesilovače už zesiluje jen asi 10x a je potřeba jej přinejmenším zkontrolovat, aby po pulzu nezakmitával a nezpůsoboval falešné detekce částic. Průběh v bodě (3) ukazuje tento obrázek.
Zákmity, které se vejdou do úrovně šumu, nevadí. Tento stupeň je napěťově navázaný na umělou zem spojenou s D_GND (napětí 4,5 až 5 V proti zemi A_GND) vytvořenou odporovým děličem (bod 5).
Detekce velikosti pulzů se v podobných konstrukcích běžně dělá tak, že mikrokontrolér cyklicky testuje napětí AD převodníkem. Jakmile napětí překročí nastavenou mez šumu, hlídá maximum až do doby, než opět poklesne pod mez do pásma šumu. Pak se zjištěné maximum zaznamená, připočte se jeden změřený pulz a zařadí. Tato metoda je jistě jednoduchá, ale vyžaduje, aby za dobu trvání pulzu bylo možné udělat a vyhodnotit nejméně 10, spíše podstatně více vzorků. Proto se programy píší co nejjednodušší a nejrychlejší v assembleru, a tomu jsem se chtěl v našich ukázkách vyhnout. Už jsme používali Arduino nebo Picaxe, nyní to ale nejde přímo, protože ani jedna z platforem nezvládá dostatečně rychle vzorkovat, stíhají sotva jeden vzorek za celou dobu trvání pulzu.
Další OZ v zapojení má za úkol zachytit maximální napětí pulzu a prodloužit jej dostatečně dlouho, aby jej AD převodník na konci měřicího intervalu mohl jedním pokusem změřit. Jakmile je napětí změřeno, mikrokontrolér krátkým pulzem otevře tranzistor a kondenzátor, který zde plní úlohu analogové paměti, vybije. Vybitím současně začíná následující měřicí perioda.
Tento princip měření předpokládá, že budou použity velmi slabé zářiče a částice budou detekovány jen řídce. Měří se v intervalech dlouhých 2 ms, nicméně na snímcích je ukázána delší perioda 5 ms. Předpokládá se, že v tomto intervalu přijde nejvýš jeden pulz. Nikdy nelze vyloučit, že jich přijde víc, v tom případě se zaregistruje napětí největšího z nich, ale měl by to být vzácný jev. Vybíjení kondenzátoru by postačovalo v délce 1 až 2 μs, dva příkazy bezprostředně po sobě následující v programu Arduina udělají pulz v délce 6,5 μs, nevadí. K vyzkoušení obvodu analyzátoru spektra stačí stíněné kontaktní pole v kovové krabičce.
Podobně jako při statistickém sledování počtu částic detekovaných GM trubicí i zde předem vytvoříme datové pole a podle změřené velikosti napětí na konci cyklu přičteme číslo 1 do příslušné buňky. Rozdíl je v tom, že každý cyklus dá nějaký nenulový výsledek přinejmenším odpovídající šumu, takže musíme stanovit mez, pod níž se napětí buď vůbec neregistruje, nebo ignoruje při vykreslení výsledku. AD převodník má referenční napětí nastavené na 3,3 V propojením vstupu REF a výstupu stabilizátoru 3,3 V. Výstup je opět v podobě grafu tvořeného znaky poslán do sériového monitoru, to nevyžaduje žádné další zařízení kromě PC již připojeného k Arduinu. I v tomto případě bude získání spektra slabého zdroje záření vyžadovat snímání po dobu desítek minut až několika hodin.
Bylo by to vlastně jednoduché, kdyby … . Je-li v okamžiku konce vybíjecího pulzu paměťového kondenzátoru napětí na neinvertujícím vstupu „prodlužovacího“ OZ kladné (je tam kladná část signálu šumu), napětí na jeho výstupu vyletí vzhůru. Jakmile vybíjecí pulz skončí, přepíše se toto napětí do kondenzátoru a v následujícím cyklu změříme falešný a většinou nezvykle velký pulz jako by přišla částice s velkou energií respektive nábojem. Tyto falešné pulzy se naštěstí dají celkem dobře rozeznat, na kondenzátoru se objeví napětí ihned po skončení vybíjení, zatímco regulérní signál se objevuje až někdy později v průběhu cyklu. Musíme si uvědomit, že doba vybíjení je v poměru k trvání cyklu asi 250x kratší. Stačí tedy ihned po vybití změřit napětí na kondenzátoru a je-li nad pásmem šumu, měřicí cyklus ani nedělat a rovnou opakovat vybíjení.
Uvedený jev nastává docela často, „vyhodíme“ až desítky procent měření, ale to nevadí. Někdy „vyhodíme“ i regulérní měření, když náhodně přišel pulz těsně po vybíjení, ale ani to nevadí, statisticky to není významné a prostě se jen posune měřicí cyklus o kousek dál v čase. Předchozí obrázek ukazuje signál v bodě 4 a stejný je pak i na výstupu. Na spodní stopě jsou vybíjecí pulzy (velmi úzké, sotva znatelné), na horní je vidět opožděný náběh napětí v průběhu cyklu (uprostřed obrazu dokonce zcela těsně před okamžikem měření a vybíjení). Vyloučení falešných pulzů funguje dobře, později jsem si ověřil, že do nasnímaných 200000 měřicích cyklů nepronikl ani jeden.
// Test spektra energie castic snimanych fotodiodou BPW34
unsigned int napeti; // promenna pro velikost pulzu
unsigned int mereni; // citac mereni kdy byl pulz
unsigned int pocetmax = 10; // po kolika pulzech se ma prekreslovat
unsigned int dolmez = 20; // dolni mez pro vykresleni - filtr sumu
unsigned long pole[128], pole2[128]; // pole pro spektrum
unsigned int grafy; // pocitadlo pro vykresleni
void setup() {
analogReference(EXTERNAL); // nastaveni reference 3,3 V
pinMode(5, OUTPUT); // vybijeni analogove pameti
for (int i = 0; i <= 127; i++) { // vynulovani pole
pole[i] = 0;
}
Serial.begin(115200); // nastaveni seriove komunikace
Serial.println(" "); // odradkovani po resetu
}
void loop() {
digitalWrite(5, HIGH); // zacatek vybijeciho pulzu
digitalWrite(5, LOW); // doba trvani 6.5 mikrosekundy
if (analogRead(0) < 80 ) { // pokud je napeti v pasmu sumu
delay(2); // doba mereni 2 ms
napeti = analogRead(0); // zmereni pulzu na konci
napeti = napeti / 4; // prevod na x meritko
if ((napeti >= dolmez) && (napeti < 127)) { // zaradit
pole[napeti]++; // pricist do pole
mereni++; // mereni je platne
grafy++; // pocitadlo pulzu do grafu
};
if (napeti >= 127) { // presahuje hodnotu
pole[127]++;
mereni++;
grafy++; // pocitadlo pulzu do grafu
};
if (grafy >= pocetmax) { // vykreslit graf?
vykresleni();
grafy = 0;
}
}
}
void vykresleni() { // vykresleni grafu
Serial.print(" Spektrum energie castic po "); // hlavicka
Serial.print(mereni);
Serial.println(" merenich");
unsigned long maximum = 0;
for (int i = 0; i <= 127; i++) { // uprava pole
pole2[i] = pole[i] / 2;
}
for (int i = dolmez; i <= 127; i++) { // hledani maxima v poli
maximum = max(maximum, pole2[i]);
}
unsigned int hodnota = maximum; // budeme vykreslovat
for (int j = maximum; j > 0; j-- ) { // od maxima po nulu
Serial.print(" +"); // levy okraj grafu
for (int i = 0; i <= 127; i++) { // vykresleni radky grafu
if ((pole2[i]) >= hodnota) {
Serial.print("#");
} else {
Serial.print(" ");
}
}
hodnota--; // pocitadlo na dalsi radek
Serial.println(" "); // konec radku
} // konec grafu - hodnot
Serial.print(" +"); // posledni radek
for (int i = 0; i < 13; i++) { // kresleni osy se znackami
Serial.print("---------+");
}
Serial.println(" "); // konec posledniho radku
Serial.println(" "); // 1 volny radek
}
Máme tedy připravené zařízení i program, ještě musíme nastavit parametry. Potřebujeme oddělit co nejtěsněji a přitom spolehlivě regulérní pulzy od šumu. Jen orientačně, jestliže má pulz na výstupu 200 mV (a to už je docela výrazný) a zesílili jsme ho asi tak 20000x, měl původně na výstupu FET tranzistoru 10 μV.
Nastavíme práh šumu téměř na nulu, měříme bez zářiče a snímáme asi tak 25000 cyklů. V nich bude minimum skutečných částic (přirozeného pozadí), uvidíme tedy spektrum šumu jako zachyceno zde.
Potom, může být i zkusmo, nastavíme práh tak, abychom šum těsně „uřízli“. Možná bude potřeba doladit parametry zobrazení aby výsledný graf byl „hezký“ a jdeme na měření. Další obrázek ukazuje spektrum energie elektronů z kontrolního zářiče SrY, vlevo zůstává viditelně prázdná oblast šumu. Výsledek (ve stejném měřítku energie) s punčoškou do lampy nebo korálky z uranového skla dopadne po hodině snímání nebo dvou dost podobně, jen několik výkyvů dává tušit nerovnoměrnosti.
Když se místo BPW34 použije dioda BPX61 s odříznutým okénkem, aby měly částice volný přístup k čipu, rozšíříme možnosti snímání spektra o detekci α částic, které se ukážou jako jasně oddělená špička v pravé části grafu vzdálená od spektra elektronů. Z poměru četnosti α a β částic pak už můžeme rozeznat různé zářiče, třeba americiový zářič z detektoru kouře ukáže téměř výhradně špičku α částic vpravo a nepatrný podíl pulzů s malou energií, zářič SrY uvedený na předchozím obrázku to má naopak. Korálky z uranového skla i punčošky do lampy vykazují oba druhy částic, ale v různém poměru.
Ještě jeden pokus a konstrukční úpravu má případně smysl udělat, ale je to trochu náročnější. Šum na výstupu snímače spektra je z drtivé většiny tvořen šumem vstupní fotodiody a její šum je úměrný pracovní teplotě. To je zřejmé. Vyplatí se chladit fotodiodu? Docílíme tím významného omezení šumu? Jaký vliv to na výsledek má ukazuje další obrázek.
Je to montáž ze dvou průběhů zaznamenaných osciloskopem, v levé polovině je výstup při teplotě kolem -18°C, v pravé při pokojové teplotě +22°C. Rozdíl 40°C redukoval šum zhruba na polovinu a tím otevřel možnost vidět mnohem víc ze spektra β částic, které se částečně do šumu schovávaly. S trochou štěstí a spoustou zkušeností se dostaneme až k detekci γ záření.
K prvnímu pokusu s vlivem teploty stačí celé zařízení umístit doma do mrazáku, nechat v klidu vytemperovat a napájení i výstup vyvést přes delší tenké kabely. Je to technicky snadné, mnohem obtížnější je přesvědčit zbytek domácnosti, že mít v mrazáku mezi zmrzlou zeleninou elektroniku snímače a radioaktivní zářič je úplně normální. Zchlazení zesilovačů samozřejmě omezuje i jejich šum, ale na výstupu se to neprojeví významným způsobem.
Chceme-li chladit méně improvizovaně, je asi nejdostupnější připevnit fotodiodu do kovového pouzdra a s ním na Peltierův článek s příkonem 5 – 10 W, samozřejmě teplo musíme na druhé straně odvést odpovídajícím aktivním chladičem. Pokud napájení Peltierova článku dělá problémy, lze se jich zbavit tím, že v krátkých periodách měření vypneme proud chlazení. Máme-li možnost sehnat malé množství, dá se experimentovat i s chlazením suchým ledem, který sublimuje při -78°C.
Pokud máte o spektrometrii větší zájem, doporučuji si projít článek na adrese http://www.rapp-instruments.de/Radioaktivitaet/Detektoren/Halbleiter/Halbleiter.htm , najdete tam schéma lepšího detektoru s OZ LF256 a vzorkovacím zesilovačem AD585, informace o tom, jak zkalibrovat detektor pomocí pulzů známé amplitudy nebo jak rozeznat původ α částic podle jejich energie. Dá se zabloudit i do oblasti amatérské rentgenové spektroskopie.
Posviťme si na ně!
Dají se nabité částice α nebo β vidět prostým okem? Přímo samozřejmě ne, ale zařízení, který to zvládne, vynalezl a postupně zdokonalil Charles Thomson Rees Wilson už na přelomu 19. a 20. století. Princip Wilsonovy mlžné (expanzní) komory je jednoduchý, v uzavřeném prostoru jsou syté páry těkavé látky, snížením tlaku je přesytíme a v tom okamžiku prolétající nabité částice fungují jako kondenzační centra, podél jejich dráhy se z kondenzovaných kapiček vytvoří mlžná stopa. Stopa se proti tmavému pozadí nejlépe zviditelní nasvícením ze strany. Sice se za okamžik rozplyne, ale i ten okamžik stačí na to, abychom zahlédli nebo dokonce vyfotografovali dráhu částice.
Ve výzkumné praxi byly už dávno mlžné komory nahrazeny komorami bublinkovými, ale to nám nebrání si jednoduchou mlžnou komoru postavit. Když se podaří vidět dráhu částic, v dalším kroku se dá se postoupit dál, nechat částice prolétat elektrickým nebo magnetickým polem a ze zakřivení dráhy odvodit jejich elektrické vlastnosti. Takto se ostatně před mnoha léty postupně dospělo k objevům v této oblasti. My máme tu výhodu, že už víme, co a jak můžeme „objevit“. Tomuto tématu se už nebudeme věnovat podrobně, jen v nástinu.
Pro amatérské mlžné komory se obvykle používá jedno ze dvou konstrukčních řešení. Buď se v utěsněné komůrce (skleničce) nechá odpařit těkavá látka (etanol, lépe isopropylalkohol) a když je vzduch uvnitř nasycený, odsaje se část objemu pryč (třeba injekční stříkačkou), tím se sníží tlak a teplota, přesytí se páry, a na krátký okamžik se zviditelní dráha částic vyletujících ze zářiče. Pak vrátíme odsátý objem zpět, počkáme na ustálení v nasyceném stavu a můžeme pozorování opakovat. Konstrukce expanzní komory je jednoduchá, ale pracuje jen krátce a cyklicky. K pozorování velmi slabých zdrojů záření (jedna částice za mnoho sekund) se moc nehodí, dobře pracuje třeba se zářičem α částic z detektoru kouře. Problémem může být i to, že při odsávání vzduchu zevnitř vniknou víry, které nám vytvořené stopy zkrátka „rozfoukají“. Příklad konstrukce i s nákresy je uveden na http://letsmakerobots.com/node/22162 .
Druhé řešení je difuzní komora, ta pracuje průběžně. Může být malá nebo i rozměrná jako stůl, je opět těsně uzavřená a jsou v ní nasycené páry isopropylu. Dno komory chladíme, u malých se používají Peltiérovy články, u větších chlazení suchým ledem nebo chladicími agregáty z mrazniček. Z druhé strany Peltiérova článku nebo lépe dvou na sobě kvůli většímu rozdílu teplot musíme teplo odvádět do chladiče, hodí se větší aktivní chladiče s teplovodivými trubicemi používané na procesorech v PC. Komora se shora zahřívá od okolí a v její horní části je i zásoba těkavé látky, odpařování může být dokonce urychleno mírným vyhříváním kapaliny. Páry klesají dolů ke dnu chlazenému na -20°C nebo nižší teplotu. V určité výšce nad černým dnem se vytvoří vrstva přesycených par, která se průběžně obnovuje a doplňuje padajícími parami shora, na dně dochází ke kondenzaci. V této vrstvě můžeme průběžně pozorovat dráhy částic vyletujících ze zářiče. Příklad konstrukce je na http://www.instructables.com/id/Make-a-Cloud-Chamber-using-Peltier-Coolers/ .
Dobře pracující a dostatečně velká mlžná komora (ve skleničce o průměru 3 cm zaregistrujeme většinou jen část nějaké stopy) s elektrickým a magnetickým polem nám dovolí dokonce i rozpoznat druh konkrétní částice, každá totiž podle svých fyzikálních vlastnosti vytváří stopy jiného tvaru, tloušťky a délky, případně se stopy mohou i větvit nebo ostře uhýbat, pokud dojde k rozpadu sledované částice. Pro začátek najdeme popis i s příklady na adrese http://www.mlznakomora.cz/mlzna-komora/ .
Závěr
Cílem tohoto dlouhého seriálu bylo ukázat, že radioaktivita (respektive ionizující záření) není něco cizího, nepřirozeného a vždy nebezpečného, jak je to někdy účelově prezentováno, ale že je to nedílná součást našeho prostředí i nás samotných. Že i s doma postaveným zařízením můžeme detekovat a do jisté míry měřit slabou aktivitu předmětů kolem nás, tím spíše potom vyšší intenzity, které už by mohly být škodlivé nebo nebezpečné. Že nemusíme být závislí na oficiálních údajích profesionálních pracovišť, ale dokážeme neviditelné záření monitorovat jednoduchými prostředky sami. To se ostatně týká i nejčastějšího případu, kdy s „radiací“ přichází nedobrovolně do styku obyvatelé domů, totiž průsaků radonu z podloží do sklepních prostor nebo aktivity stavebních materiálů vyrobených z kalů či strusky. Tomu se můžeme případně věnovat někdy příště.
Je možná rozumné bát se toho, co neznáme, ale je určitě hloupé nesnažit se poznat to, čeho se bojíme.
A to je už opravdu konec!