Úvod
Je to již nějaký čas, kdy jsme se s Martinem Pěničkou rozhodli postavit všesměrový podvozek, který jsme následně chtěli využít pro soutěž PuckCollect na RobotChallenge ve Vídni.
První diskuse byla ohledě využité geometrie. Podvozky s čtyřmi kolečky ve vzdálenosti \(l\) umístěnými symetricky vzhledem k těžisti podvozku mají větši stabilitu a lepší manevrovací schopnosti nežli podvozky se stejnou geometrií ale pouze s třemi kolečky. Avšak, s výhledem toho, že podvozek bude použitý pro PuckCollect, se varianta se čtyřmi kolečky jeví jako nepraktická, neboť potřebujete jeden otvor pro sbírání puků a další dva pro jejich uchovávání. Dohromady tedy tři boxíky. Podvozek se čtyřmi kolečky je ovšem rozdělen na čtyři části.
Dalším argumentem pro tříkolečkovou variantu je, že nepotřebujeme zvlášť přesné pozicování (odometrii), nepořebujeme vézt těžký náklad či přesně regulovat rychlost robota. Krom toho ušetříme jeden motor s enkódérem, řadič pro něj atd. Je tedy rozhodnuto. Podvozek bude postaven se třemi symetricky rozdělenými kolečky.
Tento článek jsem napsal převážně pro zvědavce o lepší odvození rovnic pro všesměrový podvozek se třemi kolečky. Jsou v něm uvedeny především výpočty a poznámky. A tedy nejde přesnou implementaci na daný HW (k čemuž snad poslouží jeden z dalších článků v budoucnosti).
Terminologie
Předem bych chtěl upozornit, že článek je psán tak, aby ho pochopil každý, kdo se již setkal se soustavou lineárních rovnic. Sem tam jsou používané odstrašující pojmy, které můžou čtenáře přesědčit o „aaaaa, tak to ne, rychle pryč“. Pokud po přečtení následujících odstavců podobný dojem získáte, věřte že není potřeba dopodrobna znát všechny zmíněné pojmy. Bohatě postačí intuitivní pohled :).
Stejně tak se nejedná o exaktní popis či přesný matematický model. Článek je sepsán tak, jak jsem o problému uvažoval. Definice pojmů, množin atd. slouží zejména k jakésy-takésy ujednání , aby nemohlo dojít k „Jéééje, je toto celé či reálné číslo?“. Abychom netápali již od začátku, přidávám malý výčet
- Budeme-li mluvit o „rychlosti koleček“, budeme míti na mysli otáčky koleček.
- Budeme-li mluvit o „\(v_i\)“, budeme míti namysli rychlosti koleček \(v_1, v_2, v_3\).
- Vektor, který má na všech pozicích jedničky budeme značit \(\vec z\).
- Nebudeme rozlišovat mezi vektorem zapsaným jako řádek a vektorem zapsaným jako sloupec.
- Mluvíme-li o souřadnicích vektoru, máme namysli souřadnice vůči kanonické/ortonormální bázi.
- V určitých částech textu můžete nalézt výrazy typu \(a = a + x\), čímž je myšleno „Vem původní hodnotu \(a\), přičti k ní \(x\) a poté výsledek ulož opět do proměnné \(a\)“.
Další drobnosti by měly být jasné z kontextu. Pokud čtenáři přijde, že některým pojmům nerozumí, či jsou špatně definovány, budu moc rád, položite-li dotaz na našem fóru.
Vlastní výpočet
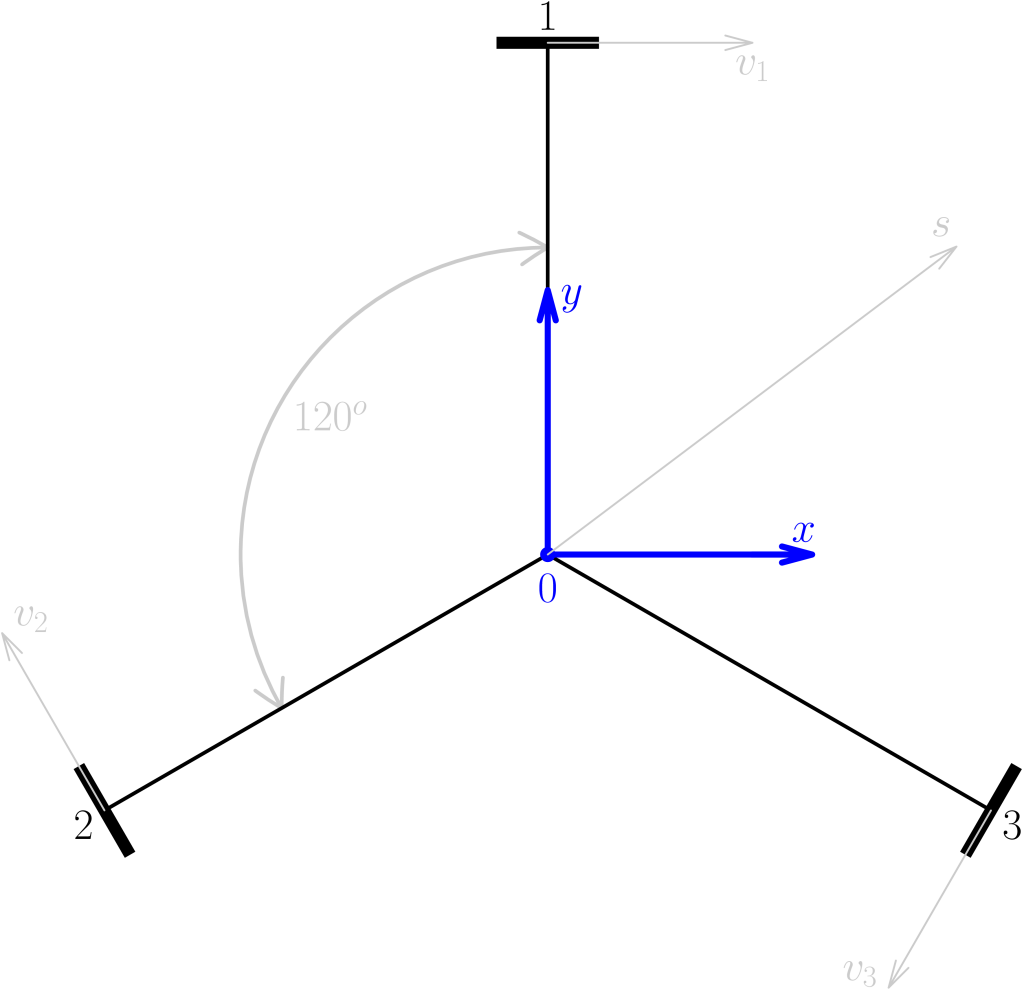
Budeme vycházet z následujícího obrázku
Popis obrázku s vysvětlením můžeme nalézt v doprovodném textu [1]. My zde uvedeme pouze rychlý suhrn
- \(\vec{s}\) – Směrový vektor ve směru, kterým se chceme pohybovat.
- \(\vec{v}_1, \vec{v}_2, \vec{v}_3\) – Vektory představující aktuální otáčky koleček.
Existuje spousta způsobů, jak vypočítat rychlosti jednotlivých koleček. Od šílených heuristik, přes primitivní promítání vektorů do směru vektoru \(\vec s\). Jelikož se mi ani jeden ze způsobů, který jsem nalezl, nelíbil, rozhodl jsem se problém vyřešit po svém (odkaz zde [1]). Ne příliš překvapivě existuje lineární zobrazení, které jednoznačně přiřadí vektoru \(\vec s\) rychlosti koleček. Označme Matici tohoto lineárního zobrazení jako \(A\) a vektor výsledných otáček jako \(\vec v = (v_1, v_2, v_3)\)
\[
\vec{v} = f(\vec{s}‘) = A \cdot
\left(
\matrix{
s_x\cr
s_y\cr
S
}
\right)
\quad
S\in\mathbb{R},
A = \left(\matrix{
2 & 0 & 1\cr
-1 & \sqrt{3} & 1\cr
-1 & -\sqrt{3} & 1
}\right)
\]
(nedá příliš velkou práci přesvědčit se, že \(A\) je regulární). Konstanta \(S\) představuje rotaci kolem osy robota. V našem případě kolem počátku soustavy. Je-li \(S\) nulové, pak k rotaci nedochází. Z rovnice výše můžeme vyjádřit rychlosti jednotlivých koleček
\[
\eqalign{
v_1 & = 2s_x+ S\cr
v_2 & = -s_x + \sqrt{3}s_y + S\cr
v_3 & = -s_x – \sqrt{3}s_y + S
}
\]
Důležité je si uvědomit, že přičtením libovolné konstanty \(x\) k velikosti \(v_1, v_2, v_3\) nerozbijeme vektor \(\vec v\), jak uvidíme níže.
Vlastnosti matice \(A\)
Každý vektor \(\vec v\), můžeme přepsat jako
\[\vec v = \vec{v}_d + S\cdot \vec z\]
Podle podmínek pro \(S\) stanovených [1] víme, že toto platí pro libovolné reálné \(S\). Uvědomíme-li si navíc, že matice \(A\) je regulární a tudíž k ní existuje matice inversní, můžeme vyjádřit \(\vec s\), \(S\) v závislosti na rychlostech jednotlivých koleček
\[
\left(\matrix{
s_x\cr
s_y\cr
S
}\right) =
{1 \over 6}\left(\matrix{
2 & -1 & -1\cr
0 & \sqrt{3} & -\sqrt{3}\cr
2 & 2 & 2\cr
}\right)\cdot
\left(\matrix{
v_1\cr
v_2\cr
v_3\cr
}\right)
\]
A hle, bobr na houbách :). Opět pozorujeme, že přičtením libovolné konstanty se vektor \(\vec s\) nezmění. Toto je velmi důležité, neboť nyní můžeme \(S\), s klidem v duši, položit rovno nule a počítat pouze s \(\vec v = \vec{v}_d\) a později rotaci prostě přičíst.
Posun daným směrem
Napřed vyřešíme problém posunu daným směrem (který je kupodivu nejsložitější). S čístým svědomím můžeme předpokládat, že všechny motorky náležící kolečkům jsou totožné. Tedy mají stejné maximální otáčky, charakteristku závislosti otáček na napětí, minimální plnění apod. Označme maximální otáčky motorků jako \(V, V \in\mathbb{N}\). Jelikož jsme vektor \(\vec s\) a konstantu \(S\) neomezili na velikosti, exituje taková kombinace \(\vec s\) a \(S\) tak, že alespoň jedno kolečko bude mít vyšší otáčky nežli \(V\). Pokud k takovéto situaci dojde, poměr mezi rychlostmi kolečet se změní a robot se nebude pohybovat žádaným směrem.
Řešení je jednoduché. Z vektoru \(\vec v\) uděláme jednotkový a vynásobíme ho \(P\cdot V\), kde \(P \in [0,1]\) a značí relativní rychlost v procentech vůči \(V\). Takto spočítaný vektor budeme značit jako \(\vec{v}_r\)
\[
\matrix{
\vec{u}_v = {1 \over |\vec v|} \cdot \vec v\cr
\vec{v}_r = PV\cdot\vec{u}_v
}
\]
Jednotlivé složky vektoru \(v\) s jistotou nebudou nikdy větší nežli \(V\).
Je nepraktické, budeme-li \(\vec s\) zadávat v kartézských souřadnicích. Daleko jednodušší bude prohlásit, že \(s\) je jednotkový vektor a bude zadán v polárních souřadnicích. Není nutné explicitně zadávat délku (\(|\vec s| = 1\)) a proto bude \(\vec s\) funkcí o jedné proměnné
\[
\vec s(\alpha) = \left(\matrix{\sin\alpha\cr \cos\alpha}\right)
\]
V úvahách výše počítáme velikost vektoru \(v\), který je zavislý na \(\vec s\). Toto může být krapet nepěkné, jelikož musíme spočítat druhé mocniny, sečíst a poté odmocnit, což pro malý mikrokontrolér nebude nic jednoduchého. Navíc těmito operacemi zvětšujeme chybu výpočtu, která je zavedena např. zaokrouhlením. Nabízí se tedy otázka, zda-li nelze výpočet velikosti \(v\) zjednodušit? Za určitých podmínek ano. Bude-li rotace nulová a velikost \(\vec s \) jedna, pak
\[
S = 0, |\vec s| = 1 \quad\Rightarrow\quad |\vec v| = \sqrt 6
\]
Důležité je podotknout, že i při pozdější započítání rotace můžeme stále využít náš trik s velikostí vektoru \(\vec v\). Vlastní důkaz zajisté provede čtenář sám :).
Pro nevěřící jsem napsal program [2]. Na výstupu dostaneme poměr mezi velikosti vypočítaného vektoru a číslem \(\sqrt 6\)
h@debian:~/$ ./size.py [alpha]
Pohyb daným směrem můžeme v kostce zapsat jako
\[
\matrix{
\eqalign{
\vec{s}(\alpha) &= \left(\matrix{\sin\alpha\cr\cos\alpha}\right)\cr
\vec{v}(\alpha) &= A \cdot \left(\matrix{\vec{s}(\alpha)\cr 0}\right)\quad\hbox{kde}\quad
A = \left(\matrix{
2 & 0 & 1\cr
-1 & \sqrt{3} & 1\cr
-1 & -\sqrt{3} & 1
}\right)\cr
\vec{u}_v &= {1\over |\vec{v}|}\cdot\vec{v} = {1\over\sqrt{6}} \cdot \vec{v}\cr
{\bf\vec{v}_r} &= {\bf PV\cdot\vec{u}_v}
}& %equalign
\qquad&\matrix{
P\in[0,1]\cr
V\in\mathbb{R}\cr
\alpha\in\mathbb{R}
} %matrix
}
\]
Nejdůležitějším je samozřejmě \(\vec{v}_r\) :).
Započítání rotace
Jelikož jsme zanedbali otáčení kolem vlastní osy robota, musíme si vytvořit manévrovací prostor, abychom mohli v případě potřeby započítat \(S\). Pro tento účel definujme konstantu \(k_s \in [0,1]\), poté
\[
\vec{v}_r = Pk_sV\cdot\vec{u}_v
\]
Označme maximální hodnotu S jako \(S_{max}\in\mathbb{R}\), a minimální hodnotu jako \(S_{min}\in\mathbb{R}\), pak
\[
\eqalign{
S_{max}&=(1-k_s)PV\cr
S_{min}&=-(1-k_s)PV
}\quad\Rightarrow \quad S\in[S_{min},S_{max}]
\]
pak vektor \(\vec v\) s započtením rotace můžeme zapsat jako
\[
\vec{v}_r = Pk_sV\cdot\vec{u}_v + S\cdot\vec z\qquad S\in[S_{min}, S_{max}]
\]
\(S\) je reálné, což není nutné a proto volme S jako celočíselné (\(S\) jsme volili reálně, abychom si při vlastním výpočtu \(A\) nesvazovali ruce).
Pokud stále pochybujete, napsal jsem další přesvědčovací prostředek, a to program [3] :).
h@debian:~/$ ./rotation.py [alpha] [P] [k_s] [S]
Započítání minimáního plnění motorů
Z valné části jsou stejnosměrné motory řízeny pomocí PWM. Z důvodu, že na malinkatých mikrokontrolelech bývá PWM implementováno dvojící timerů, budeme hodnoty generátoru ukládat jako celá čísla. Každý generátor PWM má mezní hranici, označme ji \(M_{max}\in\mathbb{N}\) a aktuální plnění PWM označme jako \(M\in[0, M_{max}]\), \(M\) je celočíselné.
Pro každý motor \((\exists! x\in[0,M_{max}])(\forall y\in\mathbb{N}, y \gt x)[V(x) = 0 \land V(x + y) \gt 0]\), kde \(V(x)\) představuje funkci, která přeloží hodnotu PWM na otáčky, více viz. sekce níže. Toto \(x\) nazveme „minimální plnění pro daný motorek“. (pozorování: takových \(x\), pro které bude platit \(V(x) = 0\) bude netriviálně mnoho, jelikož každý motorek má nenulovou „mez“, tedy minimální plnění, které potřebuje pro to, aby se osička otáčela).
Je velmi důležité takové \(x\) znát, jinak bude podvozek fungovat špatně pro netriviální množinu vektorů \(\vec s\). Pokud máme motorky od jednoho výrobce a všechny motorky mají stejnou sérii, pak můžeme toto \(x\) experimentélně zjistit pouze pro jeden, náhodně vybraný motor a spoléhat se, že ostatní motorky mají \(x\) blízké našemu, náhodně vybranému motorku.
Budeme předpokládat, že každý motorek použitý v podvozku, má stejné minimální plnění. Označme ho \(X\in[0,M_{max}]\).
Při správném nastavení \(V, k_s\) apod., můžeme rychlosti koleček považovat za hodnoty generátoru PWM. Pak souřadnice \(\vec{v}_r\)
\[
v_{ri} = v_{ri} + X\cdot sign(v_{ri})
\]
Pro lepší zápis definujme funkci signum pro vektory následně
\[\vec y = sign(\vec x)\ \Leftrightarrow\ y_i = sign(x_i)\qquad\vec x,\vec y \in \mathbb{R}^n\]
pak můžemem psát
\[\vec{v}_r = \vec{v}_r + X\cdot sign(\vec{v}_r)\]
Pozn.: Všimněme si, že jednotlivé sopuřadnice \(\vec{v}_r\) budou v netriviálním počtu případů menší nežli jedna. Nastane tak situace, kdy nebudeme využívat plný výkon motorků. Toto má jednoduché řešení. Po vlatsním výpočtu můžeme celý vektor \(\vec{v}_r\) „natáhnout“
\[
\eqalign{
v_{max} &= max(\{v_{ri}, \forall i\})\cr
\vec{v}_{r} &= (V/v_{max})\vec{v}_{r}
}
\]
Učesání výsledku
V určitém případě je lepší napřed nasimulovat, jak se naše výpočty chovají a až poté stavět robota :). Z tohoto důvodu upravíme výraz pro \(v_r\) tak, abychom mohli lépe a průhledněji stanovovat podmínky a bez obtíží simulovat i krajní případy.
Stačí pouze malá úprava. Definujeme funkci \(V\colon \mathbb{N}\to\mathbb{N}\) , pro vyjádření otáček motoru v závislosti na aktuálním „výkonu“ daného generátoru PWM
\[
\matrix{
\hbox{1.}\ \hbox{V je rostoucí}\hfill\cr
\hbox{2.}\ \forall x \in\mathbb{N}, x \le X : V(x) = 0\hfill\cr
\hbox{3.}\ \forall x \in\mathbb{N}, x \ge M_{max} : V(x) = V\hfill\cr
\hbox{4.}\ \forall x \in [0, M_{max}]\ \exists P \in [0, 1]\ : V(x) = \lceil k_sPV\rceil
}
\]
\(V\) již máme definovené výše jako maximální otáčky koleček. Pokud bude v textu zmíněno \(V\) bez kulatých závorek, jedná se o konstantu, budeli zmíněno \(V(…)\) jedná se o funkci. Výraz \(k_sPV\) můžeme nahradit funkcí \(V(M)\).
\[
\vec{v}_r = Pk_sV\cdot\vec{u}_v + S\cdot\vec z \quad\Rightarrow\quad \vec{v}_r = V(M)\cdot\vec{u}_v + S\cdot\vec z
\]
Označíme-li \(k_s,X,\vec z\) jako konstanty a uvážíme-li, že \(u_v\) je funkcí \(\alpha\), pak bude \(\vec{v}_r\) funkcí \(M,\alpha\) a \(S\), tedy
\[
\vec{v}_r(\alpha,M,S) = V(M)\cdot\vec{u}_v(\alpha) + S\cdot\vec z
\]
A opět, jakožto přesvědčovací prostředek jsem napsal program [4].
Souhrn
Podařilo se nám najít vztah mezi výkonem, který musíme pustit do motorů, směrovým vektorem, který představuje směr jímž se chceme pohybovat a rychlostmi jednotlivých koleček. Definovali jsme pár základních konstant, které nám umožnily lepší vyjádření jednotlivých veličin a nakonec si ukázali vyjádření \(\vec{v}_r\) pro postavení jednoduchého „výpočetního“ modelu :).
V jednom z dalších dílů se podíváme na jednoduchou implementaci odometrie pro všesměrový podvozek, odvození výpočtů pro podvozky s více než-li třemi kolečky a dalších drobností, souvisejících se stavbou robota pro PuckColleck. Naleznete-li své řešení pro odometrii (či N-kolečkový podvozek), neváhejte nám ho napsat na fórum i včetně případných dotazů :).
K zamyšlení
- Jak bude vypadat matice \(A\), bude-li kolečko 1 splývat s kladnou osou \(x\) místo s kladnou osou \(y\)? Lze toto nějak zobecnit, aby matice \(A\) nebyla závislá na aktualní orientaci a pozici souřadného systému vůči podvozku?
- Platí \(A^{-1} = k\cdot A^T,k\in\mathbb{R}\)?
- Jak můžeme definovat \(V\), abychom mohli bezpečně započíst minimální plnění \(X\)? (viz. sekce Započítání minimáního plnění motorů)
- Jak lze pro náš podvozek odvodit odometrii?
Materiály
Seznam matriálu, script, zajímavých odkazů…
- Scripta prof. Součka z přednášek pro „Lineární algebra pro fyziky“ na MFF UK Zimní semestr, Letní semestr. Jedná se o zápisky z přednášek. Je v nich tedy možno najít drobné chyby. Určitě se však jedná o celkem kvalitní shrnutí základů Lineární algebry.
- Stránky KSP, kde lze najít spoustu pěkných úložek a inspirace i pro programování robota 🙂
- Pěkné povídání ohledně Omniwheels a Mecanumwheels zde a zde.
- Přednášky Davida Obdržáka na MFF UK (lze zde najít, i mimo jiné, spoustu zajímavých materiálů)