Robotický podvozok zo stavebnice Totem a dielov vytlačených na 3D tlačiarni
Robotickú konštrukciu môžete postaviť buď z jednoúčelovej stavebnice, univerzálnej konštrukčnej stavebnice typu Lego Technics, Merkur, Totem, prípadne si môžete mechanické diely vytlačiť na 3D tlačiarmi. Ukážeme príklad konštrukcie robotického podvozku s využitím konštrukčnej stavebnice Totem a dielov vytlačených na 3D tlačiarni

Video ukazuje konštrukciu robotického podvozka a možnosti ovládania pomocou mobilnej aplikácie:
Pre zaujímavosť: robotický podvozok využíva riadiacu dosku Totem RoboBoard X4 využívajúcu populárnu mikrokontrolérovú platformu ESP32. Dosku RoboBoard X4 umožňuje ovládať robotickú konštrukciu mobilnou aplikáciou, alebo naprogramovať vlastnú aplikáciu vo výbojovom prostredí Arduino IDE predstavíme v samostatnom článku.

Robotický podvozok bude tvoriť kombinácia dielov konštrukčnej stavebnice Totem a dielov vytlačených na 3D tlačiarni. Tlačiť budeme diely na upevnenie motorov a predného otočného kolesa, ktoré by sa zo stavebnice konštruovali zbytočne zložito. 3D modely dielov na upevnenie motorov GM37 s priemerom 37 mm a s excentricky umiestneným hriadeľom s priemerom 6 mm sme stiahli z portálu https://www.thingiverse.com/thing:2772669.

Platformu na uchytenie predného otočného kolesa si navrhneme sami, pričom bude umožňovať mechanické pripojenie dielov stavebnice Totem
Každý majiteľ 3D tlačiarne, alebo vážny záujemca o 3D tlač skôr, či neskôr dospeje do štádia, keď mu už nestačia modely stiahnuté z internetu a chce tlačiť predmety, ktoré potrebuje. Najskôr však musí navrhnúť ich 3D model. Pri tvorbe 3D modelov môžete využiť dva princípy – vizuálny návrh, alebo vytvorenie modelu pomocou návrhového skriptu. Na tento účel odporúčame aplikáciu OpenSCAD, ktorá je k dispozícii zadarmo a stiahnete si ju z webu https://openscad.org/ . Podľa našich skúseností sa pri správnej metodike naučíte navrhovať 3D model čohokoľvek za menej ako tri hodiny.
Návrh zložitejších 3D objektov pomocou skriptu si vyžaduje lepšiu priestorovú predstavivosť. Ak ju nemáte, pomôže jednoduchá abstrakcia. Prestavte si, že vaša konštrukcia bude pozostávať z nosníkov dajme tomu o rozmeroch 1 x 1 cm potrebnej dĺžky. Takže si vytvorte modul pre nosník, ktorému zadáte ako parameter dĺžku a váš model budete vytvárať tak, že nosník za nosníkom budete postupne pomocou príkazu translate() umiestňovať do priestoru. Budete vlastne postupovať tak, ako keby ste model zostavovali z konštrukčnej stavebnice. V našom príklade je táto metóda o to názornejšia, že použijeme aj nosníky zo stavebnice Totem.
Skôr než navrhneme platformu na uchytenie predného otočného kolesa, začneme návrhom nosníka, ktorý je rozmerovo kompatibilný s nosníkmi stavebnice Totem. Dva takéto segmenty nosníkov budú súčasťou platformy a budú slúžiť na uchytenie nosníkov zo stavebnice. Nosník má rozmer 10 x 10 mm a sú v ňom otvory na skrutky M3 a otvory do ktorých sa vkladajú obdĺžnikové matice zo stavebnice Totem
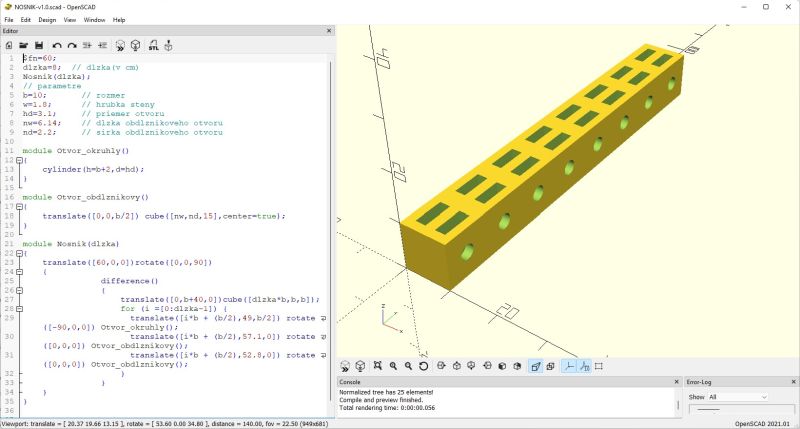
Kompletný kód návrhu nosníka:
$fn=60;
dlzka=8; // dlzka(v cm)
Nosnik(dlzka);
// parametre
b=10; // rozmer
w=1.8; // hrubka steny
hd=3.1; // priemer otvoru
nw=6.14; // dlzka obdlznikoveho otvoru
nd=2.2; // sirka obdlznikoveho otvoru
module Otvor_okruhly()
{
cylinder(h=b+2,d=hd);
}
module Otvor_obdlznikovy()
{
translate([0,0,b/2]) cube([nw,nd,15],center=true);
}
module Nosnik(dlzka)
{
translate([60,0,0])rotate([0,0,90])
{
difference()
{
translate([0,b+40,0])cube([dlzka*b,b,b]);
for (i =[0:dlzka-1]) {
translate([i*b + (b/2),49,b/2]) rotate([-90,0,0]) Otvor_okruhly();
translate([i*b + (b/2),57.1,0]) rotate([0,0,0]) Otvor_obdlznikovy();
translate([i*b + (b/2),52.8,0]) rotate([0,0,0]) Otvor_obdlznikovy();
}
}
}
}
Kód je zrozumiteľný aj pre laika. Nosník s okrúhlymi a obdĺžnikovými otvormi sa vytvorí tak, že od plného profilu kvádra potrebnej dĺžky s pôdorysom 10 x 10 mm sa pomocou príkazu difference() „odčítajú“ malé valčeky, čo sú otvory pre skrutky a na ne kolmé malé kvádre, čo sú otvory pre obdĺžnikové matice. Poloha telies v priestore je určená príkazom translate() a ich orientácia, čiže pootočenie príkazom rotate(). Na vytvorenie prázdnych priestorov v tvare valca a malého kvádra použijeme samostatné moduly, čo je ekvivalentom procedúr. Obidva typy otvorov sú rozmiestnené pravidelne 10 mm od seba, takže na tento účel použijeme jednouché cykly.
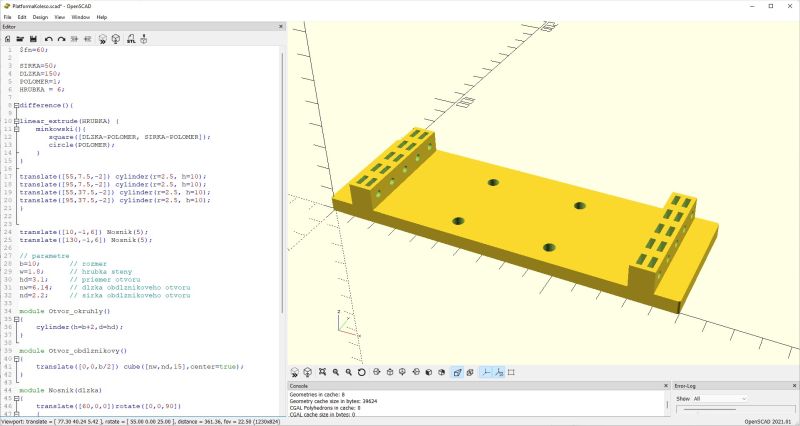
Pokračujeme návrhom platformy pre robotický podvozok na uchytenie otočného kolesa. Jej základom bude doska s jemne zaoblenými rohmi a štyrmi otvormi. Súčasťou platformy sú aj dva nosníky Je určená pre robotický podvozok na uchytenie otočného kolesa. Najskôr navrhneme dosku so zaoblenými rohmi. Určite vás napadne využiť na návrh plochého kvádra funkciu cube() my však chceme na tento objekt aplikovať funkciu minkowski() ktorá zaoblí všetky hrany, čo sa nám nehodí, pretože potrebujeme zaobliť len rohy. Preto použijeme funkciu square() na nakreslenie plochého obdĺžnika a na tento zatiaľ plochý útvar aplikujeme funkciu minkowski(), ktorá realizuje takzvaný Minkowského súčet dvoch objektov, v našom prípade štvorca a kruhu, ktorý tvorí zaoblený roh. Tento súčet množím zaviedol známy matematik Hermann Minkowski, preto bola funkcia pomenovaná po ňom.
minkowski(){
square([DLZKA, SIRKA]);
circle(POLOMER);
}
Takže máme 2D objekt, obdĺžnik so zaoblenými rohmi. Pomocou prvej ikony pod zobrazovacou plochou, alebo klávesovej skratky F5 môžeme takto navrhnutý tvar zobraziť. S využitím funkcie linear_extrude() pridáme tomuto objektu hrúbku, takže máme kváder, ktorý má zaoblené len štyri hrany, ostatné hrany sú pravouhlé. Teraz potrebujeme navrhnúť otvory. Budeme ich realizovať ako valce o vhodnom priemere, ktoré pomocou funkcie difference() „odpočítame“ od kvádra. Otvor treba príkazom translate() posunúť na správnu pozíciu. Všimnite si že valec, ktorý odoberáme je vyšší a je posunutý v osi Z nadol. Je to pre istotu aby sa nám nezobrazoval materiál o nulovej hrúbke. Parameter $fn=60 udáva jemnosť vykreslenia kružníc, ktoré sú zložené z rovných úsekov.
$fn=60;
SIRKA=50;
DLZKA=150;
POLOMER=1;
HRUBKA = 6;
difference(){
linear_extrude(HRUBKA) {
minkowski(){
square([DLZKA-POLOMER, SIRKA-POLOMER]);
circle(POLOMER);
}
}
translate([55,7.5,-2]) cylinder(r=2.5, h=10);
translate([95,7.5,-2]) cylinder(r=2.5, h=10);
translate([55,37.5,-2]) cylinder(r=2.5, h=10);
translate([95,37.5,-2]) cylinder(r=2.5, h=10);
}
translate([10,-1,6]) Nosnik(5);
translate([130,-1,6]) Nosnik(5);
// parametre
b=10; // rozmer
w=1.8; // hrubka steny
hd=3.1; // priemer otvoru
nw=6.14; // dlzka obdlznikoveho otvoru
nd=2.2; // sirka obdlznikoveho otvoru
module Otvor_okruhly()
{
cylinder(h=b+2,d=hd);
}
module Otvor_obdlznikovy()
{
translate([0,0,b/2]) cube([nw,nd,15],center=true);
}
module Nosnik(dlzka)
{
translate([60,0,0])rotate([0,0,90])
{
difference()
{
translate([0,b+40,0])cube([dlzka*b,b,b]);
for (i =[0:dlzka-1]) {
translate([i*b + (b/2),49,b/2]) rotate([-90,0,0]) Otvor_okruhly();
translate([i*b + (b/2),57.1,0]) rotate([0,0,0]) Otvor_obdlznikovy();
translate([i*b + (b/2),52.8,0]) rotate([0,0,0]) Otvor_obdlznikovy();
}
}
}
}

Rýchlo prídete na to, že abstrakcia s nosníkmi vám umožní vytvárať modely, ktoré obsahujú len nevyhnutné nosníky, takže šetríte filament a konštrukcia je pri správnom návrhu dostatočne pevná
Vo voľnom pokračovaní predstavíme riadiacu dosku Totem RoboBoard X4 využívajúcu populárnu mikrokontrolérovú platformu ESP32.

Doska umožňuje ovládanie pomocou mobilnej aplikácie aj programovanie vo vývojovom prostredí Arduino IDE
Článek byl převzat z webu Nextech se souhlasem autora.

